Alias Method概率抽奖算法C#&PHP&Java实现

最近在做抽奖服务端接口，会涉及到抽奖概率的问题，网上查资料找到一个比较好的抽奖概率的算法，Alias Method概率抽奖算法。今天就来分享一下这个算法的C#、PHP以及Java的实现。

举个例子，游戏中玩家推倒了一个boss，会按如下概率掉落物品：10%掉武器 20%掉饰品 30%掉戒指 40%掉披风。现在要给出下一个掉落的物品类型，或者说一个掉落的随机序列，要求符合上述概率。

一般会想到的两种解法

第一种算法，构造一个容量为100(或其他)的数组，将其中10个元素填充为类型1（武器），20个元素填充为类型2（饰品）…构造完毕之后，在1到100之间取随机数rand，取到的array[rand]对应的值，即为随机到的类型。这种方法优点是实现简单，构造完成之后生成随机类型的时间复杂度就是O(1)，缺点是精度不够高，占用空间大，尤其是在类型很多的时候。

第二种就是一般的离散算法，通过概率分布构造几个点，[10, 30, 60, 100]，没错，后面的值就是前面依次累加的概率之和（是不是像斐波那契数列）。在生成1~100的随机数，看它落在哪个区间，比如50在[30,60]之间，就是类型3。在查找时，可以采用线性查找，或效率更高的二分查找，时间复杂度O(logN)。

这里推荐一个大牛的两篇文章，从数学入手，探讨各种算法实现。《用JavaScript玩转游戏编程(一)掉宝类型概率》 和《实验比较各离散采样算法》 。想深入了解的朋友推荐看看。

参考他的文章中得到两个概念，PDF（密度分布函数）和 CDF（累积分布函数）两种概率分布，分别对应如上两种算法：

T	1	2	3	4
PDF	0.1	0.2	0.3	0.4
CDF	0.1	0.3	0.6	1.0

好了，现在就来说一下Alias Method（别名方法）

在这里我们不深究他的数学原理（http://www.keithschwarz.com/darts-dice-coins/ 这篇文章里详述了其原理），来看看如何使用和实现。譬如说如上的PDF[0.1,0.2,0.3,0.4]，将每种概率当做一列，别名算法最终的结果是要构造拼装出一个每一列合都为1的矩形，若每一列最后都要为1，那么要将所有元素都乘以4（概率类型的数量）

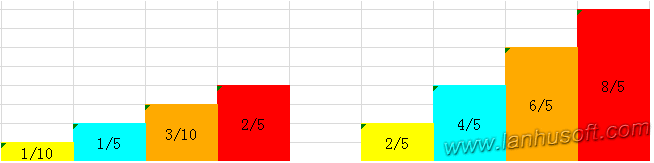
此时会有概率大于1的和小于1的，接下来就是构造出某种算法用大于1的补足小于1的，使每种概率最后都为1，注意，这里要遵循一个限制：每列至多是两种概率的组合。

最终，我们得到了两个数组，一个是在下面原始的prob数组[0.4,0.8,0.6,1]，另外就是在上面补充的Alias数组，其值代表填充的那一列的序号索引，（如果这一列上不需填充，那么就是NULL），[3,4,4,NULL]。当然，最终的结果可能不止一种，你也可能得到其他结果。

等等，这个问题还没有解决，得到这两个数组之后，随机取其中的一列，比如是第三列，让prob[3]的值与一个随机小数f比较，如果f小于prob[3]，那么结果就是3，否则就是Alias[3]，即4。

我们可以来简单验证得到的概率是不是正确的，比如随机到第三列的概率是1/4，得到第三列下半部分的概率为1/4*3/5，记得在第一列还有它的一部分，那里的概率为1/4*(1-2/5)，两者相加最终的结果还是3/10，符合原来的pdf概率。这种算法初始化较复杂，但生成随机结果的时间复杂度为O(1)，是一种性能非常好的算法。

T	1	2	3	4
PDF	0.1	0.2	0.3	0.4
Alias	3	4	4	NULL

一、Alias Method概率抽奖算法的C#实现

using System;
using System.Collections;
using System.Collections.Generic;
using System.linq;
using System.Text;
using System.Threading.Tasks;
 
namespace Lanhusoft.Core
{
    public class AliasMethod
    {
        /* The probability and alias tables. */
        private int[] _alias;
        private double[] _probability;
        
        public AliasMethod(List<Double> probabilities)
        {
 
            /* Allocate space for the probability and alias tables. */
            _probability = new double[probabilities.Count];
            _alias = new int[probabilities.Count];
 
            /* Compute the average probability and cache it for later use. */
            double average = 1.0 / probabilities.Count;
 
            /* Create two stacks to act as worklists as we populate the tables. */
            var small = new Stack<int>();
            var large = new Stack<int>();
 
            /* Populate the stacks with the input probabilities. */
            for (int i = 0; i < probabilities.Count; ++i)
            {
                /* If the probability is below the average probability, then we add
                 * it to the small list; otherwise we add it to the large list.
                 */
                if (probabilities[i] >= average)
                    large.Push(i);
                else
                    small.Push(i);
            }
 
            /* As a note: in the mathematical specification of the algorithm, we
             * will always exhaust the small list before the big list.  However,
             * due to floating point inaccuracies, this is not necessarily true.
             * Consequently, this inner loop (which tries to pair small and large
             * elements) will have to check that both lists aren't empty.
             */
            while (small.Count > 0 && large.Count > 0)
            {
                /* Get the index of the small and the large probabilities. */
                int less = small.Pop();
                int more = large.Pop();
 
                /* These probabilities have not yet been scaled up to be such that
                 * 1/n is given weight 1.0.  We do this here instead.
                 */
                _probability[less] = probabilities[less] * probabilities.Count;
                _alias[less] = more;
 
                /* Decrease the probability of the larger one by the appropriate
                 * amount.
                 */
                probabilities[more] = (probabilities[more] + probabilities[less] - average);
 
                /* If the new probability is less than the average, add it into the
                 * small list; otherwise add it to the large list.
                 */
                if (probabilities[more] >= average)
                    large.Push(more);
                else
                    small.Push(more);
            }
 
            /* At this point, everything is in one list, which means that the
             * remaining probabilities should all be 1/n.  Based on this, set them
             * appropriately.  Due to numerical issues, we can't be sure which
             * stack will hold the entries, so we empty both.
             */
            while (small.Count > 0)
                _probability[small.Pop()] = 1.0;
            while (large.Count > 0)
                _probability[large.Pop()] = 1.0;
        }
 
        /**
         * Samples a value from the underlying distribution.
         *
         * @return A random value sampled from the underlying distribution.
         */
        public int next()
        {
 
            long tick = DateTime.Now.Ticks;
            var seed = ((int)(tick & 0xffffffffL) | (int)(tick >> 32));
            unchecked
            {
                seed = (seed + Guid.NewGuid().GetHashCode() + new Random().Next(0, 100));
            }
            var random = new Random(seed);
            int column = random.Next(_probability.Length);
 
            /* Generate a biased coin toss to determine which option to pick. */
            bool coinToss = random.NextDouble() < _probability[column];
 
            return coinToss ? column : _alias[column];
        }
    }
}

二、Alias Method概率抽奖算法的PHP实现

<?php  
class AliasMethod  
{  
    private $length;  
    private $prob_arr;  
    private $alias;  
  
    public function __construct ($pdf)  
    {  
        $this->length = 0;  
        $this->prob_arr = $this->alias = array();  
        $this->_init($pdf);  
    }  
    private function _init($pdf)  
    {  
        $this->length = count($pdf);  
        if($this->length == 0)  
            die("pdf is empty");  
        if(array_sum($pdf) != 1.0)  
            die("pdf sum not equal 1, sum:".array_sum($pdf));  
  
        $small = $large = array();  
		$average=1.0/$this->length;
        for ($i=0; $i < $this->length; $i++)   
        {   
            $pdf[$i] *= $this->length;  
            if($pdf[$i] < $average)  
                $small[] = $i;  
            else  
                $large[] = $i;  
        }  
  
        while (count($small) != 0 && count($large) != 0)   
        {  
            $s_index = array_shift($small);  
            $l_index = array_shift($large);  
            $this->prob_arr[$s_index] = $pdf[$s_index]*$this->length;  
            $this->alias[$s_index] = $l_index;  
  
            $pdf[$l_index] += $pdf[$s_index]-$average;  
            if($pdf[$l_index] < $average)  
                $small[] = $l_index;  
            else  
                $large[] = $l_index;  
        }  
  
        while(!empty($small))  
            $this->prob_arr[array_shift($small)] = 1.0;  
        while (!empty($large))  
            $this->prob_arr[array_shift($large)] = 1.0;  
    }  
    public function next_rand()  
    {  
        $column = mt_rand(0, $this->length - 1);  
        return mt_rand() / mt_getrandmax() < $this->prob_arr[$column] ? $column : $this->alias[$column];  
    }  
}  
?>  

三、Alias Method概率抽奖算法的Java实现

package com.lanhusoft.rsaapp;
 
import android.util.Log;
 
import java.util.*;
import java.util.concurrent.atomic.AtomicInteger;
 
 
public final class AliasMethod {
    /* The random number generator used to sample from the distribution. */
    private final Random random;
 
    /* The probability and alias tables. */
    private final int[] alias;
    private final double[] probability;
 
    /**
     * Constructs a new AliasMethod to sample from a discrete distribution and
     * hand back outcomes based on the probability distribution.
     * <p/>
     * Given as input a list of probabilities corresponding to outcomes 0, 1,
     * ..., n - 1, this constructor creates the probability and alias tables
     * needed to efficiently sample from this distribution.
     *
     * @param probabilities The list of probabilities.
     */
    public AliasMethod(List<Double> probabilities) {
        this(probabilities, new Random());
    }
 
    /**
     * Constructs a new AliasMethod to sample from a discrete distribution and
     * hand back outcomes based on the probability distribution.
     * <p/>
     * Given as input a list of probabilities corresponding to outcomes 0, 1,
     * ..., n - 1, along with the random number generator that should be used
     * as the underlying generator, this constructor creates the probability
     * and alias tables needed to efficiently sample from this distribution.
     *
     * @param probabilities The list of probabilities.
     * @param random        The random number generator
     */
    public AliasMethod(List<Double> probabilities, Random random) {
        /* Begin by doing basic structural checks on the inputs. */
        if (probabilities == null || random == null)
            throw new NullPointerException();
        if (probabilities.size() == 0)
            throw new IllegalArgumentException("Probability vector must be nonempty.");
 
        /* Allocate space for the probability and alias tables. */
        probability = new double[probabilities.size()];
        alias = new int[probabilities.size()];
 
        /* Store the underlying generator. */
        this.random = random;
 
        /* Compute the average probability and cache it for later use. */
        final double average = 1.0 / probabilities.size();
 
        /* Make a copy of the probabilities list, since we will be making
         * changes to it.
         */
        probabilities = new ArrayList<Double>(probabilities);
 
        /* Create two stacks to act as worklists as we populate the tables. */
        Deque<Integer> small = new ArrayDeque<Integer>();
        Deque<Integer> large = new ArrayDeque<Integer>();
 
        /* Populate the stacks with the input probabilities. */
        for (int i = 0; i < probabilities.size(); ++i) {
            /* If the probability is below the average probability, then we add
             * it to the small list; otherwise we add it to the large list.
             */
            if (probabilities.get(i) >= average)
                large.add(i);
            else
                small.add(i);
        }
 
        /* As a note: in the mathematical specification of the algorithm, we
         * will always exhaust the small list before the big list.  However,
         * due to floating point inaccuracies, this is not necessarily true.
         * Consequently, this inner loop (which tries to pair small and large
         * elements) will have to check that both lists aren't empty.
         */
        while (!small.isEmpty() && !large.isEmpty()) {
            /* Get the index of the small and the large probabilities. */
            int less = small.removeLast();
            int more = large.removeLast();
 
            /* These probabilities have not yet been scaled up to be such that
             * 1/n is given weight 1.0.  We do this here instead.
             */
            probability[less] = probabilities.get(less) * probabilities.size();
            alias[less] = more;
 
            /* Decrease the probability of the larger one by the appropriate
             * amount.
             */
            probabilities.set(more,
                    (probabilities.get(more) + probabilities.get(less)) - average);
 
            /* If the new probability is less than the average, add it into the
             * small list; otherwise add it to the large list.
             */
            if (probabilities.get(more) >= 1.0 / probabilities.size())
                large.add(more);
            else
                small.add(more);
        }
 
        /* At this point, everything is in one list, which means that the
         * remaining probabilities should all be 1/n.  Based on this, set them
         * appropriately.  Due to numerical issues, we can't be sure which
         * stack will hold the entries, so we empty both.
         */
        while (!small.isEmpty())
            probability[small.removeLast()] = 1.0;
        while (!large.isEmpty())
            probability[large.removeLast()] = 1.0;
    }
 
    /**
     * Samples a value from the underlying distribution.
     *
     * @return A random value sampled from the underlying distribution.
     */
    public int next() {
        /* Generate a fair die roll to determine which column to inspect. */
        int column = random.nextInt(probability.length);
 
        /* Generate a biased coin toss to determine which option to pick. */
        boolean coinToss = random.nextDouble() < probability[column];
 
        /* Based on the outcome, return either the column or its alias. */
       /* Log.i("1234","column="+column);
        Log.i("1234","coinToss="+coinToss);
        Log.i("1234","alias[column]="+coinToss);*/
        return coinToss ? column : alias[column];
    }
 
    public static void main(String[] args) {
        TreeMap<String, Double> map = new TreeMap<String, Double>();
        map.put("1金币", 0.2);
        map.put("2金币", 0.15);
        map.put("3金币", 0.1);
        map.put("4金币", 0.05);
        map.put("未中奖", 0.5);
 
        List<Double> list = new ArrayList<Double>(map.values());
        List<String> gifts = new ArrayList<String>(map.keySet());
 
        AliasMethod method = new AliasMethod(list);
 
        Map<String, AtomicInteger> resultMap = new HashMap<String, AtomicInteger>();
 
        for (int i = 0; i < 100000; i++) {
            int index = method.next();
            String key = gifts.get(index);
            if (!resultMap.containsKey(key)) {
                resultMap.put(key, new AtomicInteger());
            }
            resultMap.get(key).incrementAndGet();
        }
        for (String key : resultMap.keySet()) {
            System.out.println(key + "==" + resultMap.get(key));
        }
 
    }
}

文章转载自：蓝狐软件工作室 » C#&PHP&Java实现Alias Method概率抽奖算法